After finishing my last post on the headphone DSP chain, I intended to write the second part which should provide examples of adjusting the parameters of the chain effects for particular models of headphones. However, while writing it I had encountered some curious behavior of the mid/side equalization module, and decided to figure out what's going on there and write about it.
Let's recall last part of the DSP chain that I have proposed previously. Note that I've changed the order of the effects application, I will explain the reason at the end of the post:
The highlighted part is the pair of filters which apply diffuse field to free field (df-to-ff) or vice versa (ff-to-df) correction EQ curves to mid and side components separately. To remind you, these are intended to help the brain to disambiguate between "in front of the head" and "behind the head" audio source positions, with a goal to improve externalization. As I've found, well made headphones likely only need just one of the corrections applied. For example, if the headphones are tuned closer to the "diffuse field" target, then they already should reproduce "behind the head" and "around you" sources realistically, however, frontal sources could be localized "inside the head." For such headphones, applying a df-to-ff compensation to the "mid" component helps to "pull out" frontal sources from inside the head and put them in the front. Conversely, for the headphones tuned with a preference for the "free field," it's beneficial to apply "ff-to-df" correction to the side component of the M/S representation in order to make surrounding and "behind the head" sources to be placed correctly in the auditory image.
Now, a discovery which was surprising for me was that the application of a mid/side equalization affects reproduction of unilateral (existing in one channel only) signals. A test signal sent to the left channel exclusively, was creating a signal in the right channel as a result of passing through the mid/side equalizer. And that's even with all cross-feeding turned off, of course. This had caught me by surprise because I knew that converting between stereo and mid/side representations should be lossless and that also assumes that no signals appear out of nowhere. So, what's going on here?
The Sinusoids Algebra
What I have realized is that all this behavior appears to be surprising at first only because addition and subtractions of audio signals is in fact not very intuitive. In order to get a good grasp of it, I went through Chapter 4 of Bob MacCarthy's book "Sound Systems: Design and Optimization". It provides a very extensive and insightful coverage with just a minimal help of math. I think, it's worth stating here some facts from it about summing of two sinusoidal signals of the same frequency:
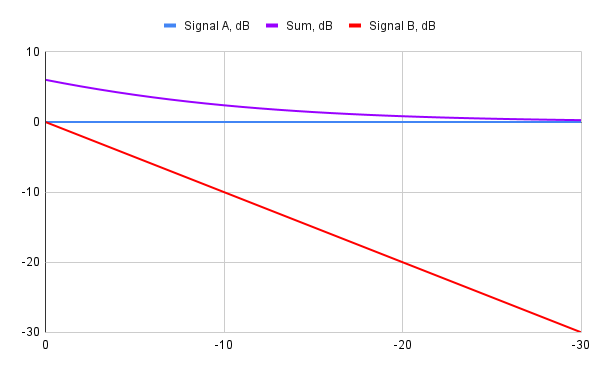
- When adding signals of different amplitudes, it's the amplitude of the loudest signal, and the difference between amplitudes that matter the most. The phase of the weaker signal is of a lesser significance. There is a formula to express this fact: Sum = 20*Log10((A + B) / A) (A is the level of the louder signal). Graphically the resulting levels for in-phase signals summation look like this:
Only when adding or subtracting signals that have similar amplitudes their relative phase (we can also say the "phase shift") starts to matter.
There is no linear symmetry between the case when the two added signals of the same amplitude are in phase, and the case when they are completely out of phase. In the first case the amplitude doubles, whereas in the second case they fully cancel each other out. People who ever tried building their own loudspeakers are well aware of this fact. This is the graphical representation of the resulting amplitude depending on the phase shift:
Another thing worth understanding is how the inter channel correlation coefficient (ICCC) depends on the relationship between the signals. This is the "correlation" gauge which we observe in plugins dealing with M/S manipulations. What plugins typically show is the correlation at the "zero lag," that is, when there is no extra time shift between the signals (in addition to the shift they already have).
As a side note, a lot of times the calculation of cross-correlation is carried out in order to find how much one signal needs to be shifted against another in time in order to achieve the maximum match. That's why "lag" is considered. By the way, here is a nice interactive visualization of this process by Jack Schaedler. However, for the purpose of calculating the ICCC we only consider the case of non-shifted signals, thus the "lag" is 0.
In the case of zero lag, the correlation can be calculated simply as a dot product of two signals expressed as complex exponentials: A(t)*B̅(t), where B̅ denotes a complex conjugate of B. Since we deal with the same signal, and its version shifted in phase, the parameters for the frequency mutually cancel each other, and what we left with is just the cosine of the phase shift. That should be intuitively clear: for signals in phase, that is, with no phase shift, the ICCC is cos(0)=1.0, for signals completely out of phase (phase shift π/2) the correlation is cos(π/2)=0, and finally, when the first signal is phase inverted compared to the second one, the ICCC is cos(π)=-1.0.
By the way, since we deal with a "normalized" correlation, that is, having the value between -1.0 and 1.0, the ICCC does not depend on the relative amplitude of the signals. Thus, for example, in-phase signals of the same amplitude have the same ICCC as in-phase signals with a relative level of -60 dB. Strictly speaking, when there is no signal with matching frequency in another channel, their correlation is not defined, however, for simplicity plugins show the ICCC of 0 in this case.
ICCC and Mid/Side Signal Placement
From the previous fact, it can be seen that ICCC actually does not fully "predict" how a pair of signals in the left and the right channel will end up being placed in the Mid/Side representation. That's because ICCC only reflects their phase shift, while the result of summation also depends on their relative levels. For a better understanding of relationship between the stereo and M/S representations we need a two-dimensional factor, and the visual representation of this factor is what the tool called "goniometer" shows. I will use it when talking about my test signals and tracks in the next post.
To round up what we have just understood, let's consider the process of making the M/S representation of an input stereo signal. If we consider each frequency separately, then we can apply the facts stated above to each pair of individual sinusoids from the left and the right channel. This adds more details to a somewhat simplistic description I provided in the previous post.
If the sinusoid in one of the channels is much higher in the amplitude than in another channel, then both summation and subtraction will produce a signal which is very similar to the stronger source signal, and the weaker signal will only make a small contribution to the result, regardless of its relative phase.
That means, a strong unilateral signal will end up being both in the "mid" and the "side" components, minimally affected by the signal of the same frequency from the opposite stereo channel. Note that if we normalize the resulting amplitudes of the "Mid" and "Side" signals by dividing them by 2, we will actually see a signal of a lower amplitude there. Here is an illustration—an example stereo signal is on the top, it has the level of the right channel lower by -12 dB. The resulting "Mid Only" and "Side Only" versions are below it:
In the case when there is no signal of this frequency in the opposite channel, then exactly the same signal will land both into both M/S components, with the amplitude divided by 2. This is the picture from the previous post showing that for the two sinusoids in the middle of the top picture:
If both channels of the input stereo signal contain the signal of a particular frequency with close enough amplitudes, then the outcome depends on the relative phase between these signals. As we know, in the "extreme" cases of fully correlated or fully anti-correlated signals, only the mid or the side component will end up carrying this frequency (this was also shown on a picture in the previous post). For all the cases of the phase lying in between, the result will get spread out between the mid and the side, below is an example for the case of a 140 deg phase offset (ICCC=-0.766) which results in a -12.6 dB reduction of the original signal level as a result of summation:
Note that the resulting sinusoids in the mid and the side channels have a phase shift from the signal in the left channel which is different both from what the signal in the right channel has, and from each other.
Since the process of decoding the stereo signal from the M/S representation is also done via addition and subtraction, the same sinusoids algebra applies to it as well.
What If We Change Just Mid or Side?
It's interesting that despite the fact that separate mid/side equalization is an old technique used by both mixing and mastering engineers, thanks to its benefits for the ear, it's side effects on the signal are not described as widely. However, if you read the previous section carefully, you now understand that making level and phase adjustments to the mid or to the side components only will inevitably affect the outcome of "decoding" the M/S representation back into stereo.
For simplicity, let's focus on amplitude changes only. Making changes both in amplitude and phase will cause even more complex effects when the signals get summed or subtracted. That means, we apply a "linear phase" equalizer. We can use either an equalizer which provides mid/side equalization directly, for example: the "LP10" plugin by DDMF, or "thEQorange" by MAAT digital. However, in fact, we can use any linear phase equalizer which provides two independently controlled channels because we can wrap it between two instances of the MSED plugin: the first one needs to "encode" stereo into the M/S representation, and the second one will produce the stereo version back from the modified signal, as shown below:
(even though MSED is completely free, if you want an alternative for some reason, there is also the "Midside Matrix" plugin by Goodhertz, also free).
Since no equalizer can affect just a single frequency only, instead of looking at sinusoiods in the time domain as we will switch into the frequency domain. My approach to testing here is to use the same log sweep in the both channels, and modify either amplitude of relative phase of the second channel, as we did before. Then I capture what comes out in the left and the right channel after an EQ applied separately to the Mid or the Side representation.
I start with the case which had initially drawn my attention: a unilateral stereo signal (in the left channel only) for which we apply some equalization to the mid component. Let's see what do left and right channels contain after we apply a simple +10 dB, Q 5 gain to the 920 Hz center frequency to the mid component only:
As you can see, indeed after this equalization a signal has appeared in the right channel! Another interesting observation is that the level of the gain for the unilateral signal is actually less than +10 dB. That's because the gain that we have applied to the mid component was combined with the unmodified (flat) signal from the side component. Only in the case when there was no side component at all—identical signals in the left and the right stereo channels—the equalization of the mid component will look like a regular stereo equalization. Certainly, it is good to be aware of that!
By the way, I tried both LP10 and thEQOrange and their behavior is the same. Considering that LP10 costs just about $40, and thEQOrange almost 15 times more, it's good to know that you can get away with a cheaper option unless you strongly prefer the UI of thEQOrange.
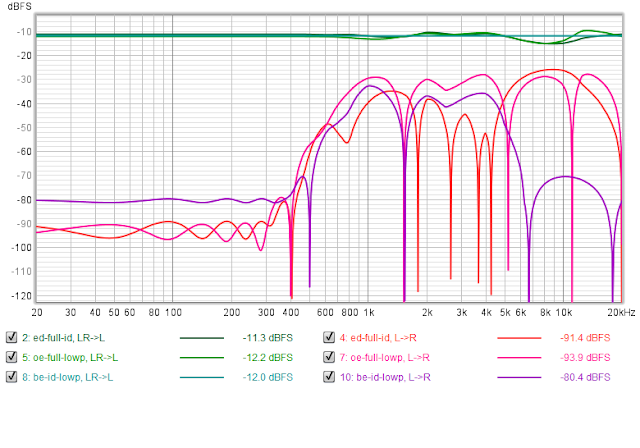
Now, I was genuinely interested in seeing what my FF-to-DF and DF-to-FF Mid/Side equalization do to unilateral signals. Here are some examples comparing the effect on the fully correlated signal (shades of green) with the signal induced in the opposite channel for a unilateral input:
We can see that in some cases the levels of signals induced in the opposite channel are significant and can be only -15 dB lower than the "main" signal. However, we need to recall that the FF/DF compensation comes after we have applied the cross-feed unit. That means, we never really have unilateral stereo signals. To check what actually happens, I put the "direct" path processing in front of the FF/DF unit and used the same initially unilateral test signals. This is what I've got:
These curves definitely look less frightening. Thanks to crossfeed, any unilateral signal penetrates into the opposite channel.
Conslusions
What have we learned from this lengthy exploration? First, it's soothed my worries about the side effects of the Mid/Side equalization. Since I only use it with much more correlated signals than the edge case of a unilateral stereo signal, the side effects are not as significant, while the win of the FF/DF compensation is audibly perceivable.
Second, looking closer at what happens during the M/S equalization helped me to reveal and fix two issues with my initial chain topology:
I reordered the units in the output chain, putting the FF/DF unit before the L/R band alignment unit. That's because I have realized that individual equalization of the left and the right channels inevitably affects the contents of the mid/side representation. For example, a signal which initially was identical between the left and the right channels will obviously lose this property after going through an equalizer which applies different curves to the left and the right channels.
Since for the FF/DF I actually use the MConvolutionEZ plugin—with a linear phase filter—I noticed that the approach of applying the convolution to the mid and side components recommended in the manual does not work well for my case. What MeldaProduction recommends is to chain two instances of MConvolutionEZ: one in "Mid" mode and one in "Side" mode one after another. This in fact creates a comb filter because mid and side are now processed with a one sample delay, and then get summed (I did confirm that). So instead of doing that, I wrapped MConvolutionEZ between two instances of MSED (as I've shown above) and just use it in the regular "stereo" mode. This ensures that both mid and side are processed with no time difference.
I also considered, if it's possible to create a Mid/Side equalization which avoids processing of sufficiently uncorrelated signals in order to avoid the side effects described above. A search for "correlation-dependent band gain change" led me to a bunch of microphone beamforming techniques. Indeed, in beamforming we want to boost the frequency bands that contain correlated signals, and diminish uncorrelated signals (noise). However, thinking about this a bit more, I realized that such processing becomes dependent on the signal, and thus isn't linear anymore. As we saw previously with my analysis of the approaches for automatic gain control such signal-dependent processing can add significant levels of non-linear distortion. That's probably why even sufficiently expensive mastering equalizers don't try to fight the side effects of mid/side equalization.








No comments:
Post a Comment