Providing another update on my ongoing project of the DIY stereo spatializer for headphones. A couple of months ago my plan was to write a post with a guide for setting up parameters of the blocks of the chain. However, as usual, some experiments and theoretical considerations introduced significant changes to the original plan.
Spatial Signal Analysis
Since the times when I started experimenting with mid-side processing, I realized that measurements that employ sending the test signal to one channel only must be accompanied by measurements that send it to both channels at the same time. Also, the processed output inevitably appears on both channels of binaural playback chain, and thus they both must be captured.
Because of this, whenever I measure a binaural chain, I use the following combinations of inputs and outputs:
- Input into left channel, output from the left channel, and output from the right channel: L→L and L→R. And if the system is not perfectly symmetric, then we also need to consider R→R and R→L.
- Correlated input into both channels (exactly the same signal), output from the left and the right channel: L+R→L, L+R→R.
- Anti-correlated input into both channels (one of the channels reversed, I usually reverse the right channel): L-R→L, L-R→R. I must note that for completeness, I should also measure R-L→L and R-L→R, but I usually skip these in order to save time. Also note that in an ideal situation (identical L and R signals, ideal summing), the difference would be zero. However, as we will see, in a real acoustical environment it is very far from that.
So, that's 8 measurements (if we skip R-L→L and R-L→R). In addition to these, it is also helpful to look at the behavior of reverberation. I measure it for L→L and R→R real or simulated acoustic paths.
Now, in order to perform the analysis, I create the following derivatives using "Trace Arithmetic" in REW:
- If reverb (real or simulated) is present, I apply FDW window of 15 cycles to all measurements.
- Apply magnitudes spectral division (REW operation "|A| / |B|") for L→R over L→L, and R→L over R→R. Then average (REW operation "(A + B) / 2") the results and apply psychoacoustic smoothing. This is the approximate magnitude of the crossfeed filter for the contra-lateral channel.
- Apply magnitudes spectral division for L+R→L over L→L, and L+R→R over R→R. Then also average and smooth. This is the relative magnitude of the "phantom center" compared to purely unilateral speaker sources.
- Finally, apply magnitudes spectral division for L-R→L over L+R→L, L-R→R over L+R→R, average and smoothen the result. This shows the relative magnitude of the "ambient component" compared to the phantom center.
The fact that we divide magnitudes helps to remove the uncertainties of the measurement equipment and allows comparing measurements taken under different conditions. This set of measurements can be called "spatial signal analysis" for the reason that it actually helps to understand how the resulting 3D audio field will be perceived by a human listener.
I have performed this kind of analysis both for my DIY spatializer chain, and also for my desktop speaker setup (using binaural microphones), and for comparison purposes, with Apple's spatializer over AirPods Pro (2nd gen), in "Fixed" mode, personalized for me using their wizard. From my experience, the analysis seems to be quite useful in understanding the reasons why I hear the test tracks (see the Part II of the series) this or that way on a certain real or simulated audio setup. It also helps in revealing flaws and limitations of the setups. Recalling the saying by Floyd Toole that a measurement microphone and a spectrum analyzer is not a good substitute for human ears and the brain, I would like to believe that binaural measurement like this one, although still imperfect, does in fact model the human perception much closer.
Updated Processing Chain
Unsurprisingly, after measuring different systems and comparing the results, I had to correct the topology of the processing chain (the initial version was introduced in the Part I). The updated diagram is presented below, and the explanations follow it:
Compared to the original version, there are now 4 parallel input "lanes" (on the diagram, I have grouped them in 2x2 formation), and their function and the set of plugins comprising them is also different. Obviously, the most important component—the direct sound is still there, and similarly to the original version of the chain, the direct sound remains practically unaltered, except for adjusting the level of the phantom "center" compared to pure left and right and ambient components. By the way, instead of Mid/Side plugin I switched to "Phantom Center" plugin by Bertom Audio. The second lane is intended to control the level and the spectral shape of the ambient component.
Let me explain this frontend part before we proceed to the rest of the chain. After making the "spatial analysis" measurements, I realized that in a real speaker setup, the ambient component of the recording is greatly amplified by the room, and depending on the properties of the walls, it can even exceed in level "direct" signal sources. On measurements, this can be seen by comparing the magnitudes of uncorrelated (L→L, R→R), correlated (L+R→L, L+R→R), and anti-correlated (L-R→L, L-R→R) sets. The human body also plays an important role as an acoustical element here, and the results of measurements done using binaural microphones differ drastically from "traditional" measurements using a measurement microphone on a stand.
As a result, the ambient component has received a dedicated processing lane, so that its level and the spectral shape can be adjusted individually. By the way, in the old version of the chain, I used the Mid/Side representation of the stereo signal in order to tune the ambient sound component independently of the direct component. In the updated version, I switched to a plugin which extracts the phantom center based on the inter-channel correlation. As a result, pure unilateral signals are separated from the phantom center (recall from my post on Mid/Side Equalization that the "Mid" component still contains left and right, albeit in a reduced level compared to the phantom center).
Continuing on the chain topology, the output from the input lanes is mixed and is fed to the block which applies Mid/Side Equalization. This block replaces the FF/DF block I was using previously. To recap, the old FF/DF block was tuned after the paper by D. Hammershøi and H. Møller, which provides statistically averaged free-field and diffuse-field curves from binaural measurements of noise loudness on human subjects, compared to traditional noise measurements with a standalone microphone. The new version of the equalization block in my chain is derived from actual acoustic measurement in my room, on my body. Thus, I believe, it represents my personal characteristics more faithfully.
Following the Direct/Ambient EQ block, there are two parallel lanes for simulating binaural leakage and reproducing the effect of the torso reflection. This is part of the crossfeed unit, yet it's a bit more advanced than a simple crossfeed. In order to be truer to human anatomy, I added a delayed signal which mimics the effect of the torso reflection. Inevitably, this creates a comb filter, however this simulated reflection provides a significant effect of externalization, and also makes the timbre of the reproduced signal more natural. With careful tuning, the psychoacoustic perception of the comb filter can be minimized.
I must say, previously I misunderstood the secondary peak in the ETC which I observed when applying the crossfeed with the RedLine Monitor while having the "distance" parameter set to a non-zero value. Now I see that it is there to simulate the torso reflection. However, the weak point of such a generalized simulation is that the comb filter created with this reflection can be easily heard. In order to hide it, we need to adjust the parameters of the reflected impulse: the delay, the level, and the frequency response to match more naturally the properties of our body. After this adjustment, the hearing system starts naturally "ignoring" it, effectively transforming it into a perception of "externalization," same as it happens with the reflection from our physical torso. Part of adjustment that makes this simulated reflection more natural is making it asymmetric. Obviously, our physical torso and the resulting reflection is asymmetric as well.
Note that the delayed paths are intentionally band-limited to simulate partial absorption of higher frequencies of the audible range by parts of our bodies. This also inhibits the effects of comb filtering on the higher frequencies.
The output from the "ipsi-" and "contralateral" blocks of the chain gets shaped by crossfeed filters. If you recall, previously I came up with a crossfeed implementation which uses close to linear phase filters. I still use the all-pass component in the new chain, for creating the group delay, however, the shape of the magnitude response of the filter for the opposite (contralateral) ear is now more complex, and reflects the effect of the head diffraction.
And finally, we get to the block which adjusts the output to particular headphones being used. For my experiments and for recreational listening I ended up using Zero:Red IEMs by Truthear due to their low distortion (see the measurements by Amir from ASR) and "natural" frequency response. Yet, it is not "natural" enough for binaural playback, and still need to be adjusted.
Tuning the Processing Chain
Naturally, there are lots of parameters in this chain, and tuning it can be a time-consuming, yet captivating process. The initial part of tuning can be done objectively, by performing the "spatial signal analysis" mentioned before and comparing the results between different setups. It's unlikely that any of the setups is "ideal," and thus the results need to be considered with caution and shouldn't be just copied blindly.
Another reason why blind copying is not advised is due to uncertainties of the measurement process. From the high level point of view, a measurement of the room sound via binaural microphones blocking the ear canal should be equivalent to the sound that arrives to ear-blocking IEMs by wires. Conceptually, IEMs will just propagate the sound further, to the ear drum. The problem is that a combination of arbitrary mics and arbitrary IEMs create a non-flat "insertion gain." I could easily check that by making a binaural recording and then listening to it via IEMs—it's "close," but still not fully realistic. Ideally, a headset with mics should be used which was tuned by the manufacturer to achieve a flat insertion gain. However, in practice it's very hard to find a good one.
Direct and Ambient Sound Field Ratios
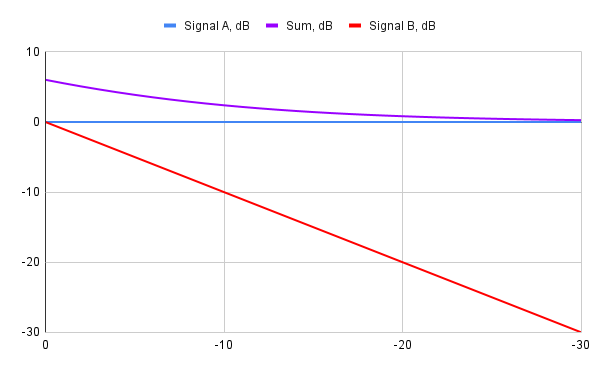
Initially, I've spent some time trying to bring the ratios between correlated and uncorrelated components, and the major features of their magnitude response differences to be similar to my room setup. However, I was aware that the room has too many reflections, and too much uncorrelated sound resulting from it. This is why the reproduction of "off-stage" positions from the test track described in the part II of the blog post series has some technical flaws. Nevertheless, let's take a look at these ratios. The graph below shows how the magnitude response of fully correlated (L+R) components differ from uncorrelated direct paths (L→L, R→R), averaged, and smoothed psychoacoustically (as a reminder, this is a binaural measurement using microphones that block the ear canal):
We can see that the bass sums up and becomes louder than individual left and right channels by 6 dB—that's totally unsurprising because I have a mono subwoofer, and the radiation pattern of LXmini speakers which I used for this measurement is omnidirectional at low frequencies. As the direction pattern becomes more dipole-like, the sound level of the sum becomes closer to the sound level of an individual speaker. Around 2 kHz the sum even becomes quieter than a single channel—I guess this is due to acoustical effects of the head and torso. However, the general trend is what one would expect—two speakers play louder than one.
Now let's take a look at the magnitude ratio between the anti-correlated, "ambient" component, and fully correlated sound. Basically, the graph below shows the magnitude response of the filter that would turn the direct sound component into the ambient component:
It's interesting that in theory, anti-correlated signals should totally cancel each other. However, that only happens under ideal conditions, like digital or electrical summing—and that's exactly what we see below 120 Hz due to the digital summing of the signals sent to the subwoofer. But then, as the signal switches to stereo speakers, there is far less correlation, and cancellation does not occur. In fact, due to reflections and head refraction, these initially anti-correlated (at the electrical level) signals become more correlated, and can even end up having higher energy than correlated signal, when summed. Again, we see that around the 2 kHz region, and then, around 6.5 kHz, and 11 kHz.
The domination of the ambient component can actually be verified by listening. To confirm it, I used my narrow-banded mono signals, and created an "anti-correlated" set by inverting the right channel. Then I started playing through speakers pairs of correlated and anti-correlated test signals for the same frequency band—and indeed—sometimes the anti-correlated pair sounded louder! However, the question is—should I actually replicate this behavior in the headphone setup, or not?
The dominance of the ambient (diffuse) component over direct (free-field) component around 6.5 kHz and 11 kHz agrees with the diffuse-field and free-field compensation curves from the Hammershøi and Møller paper I mentioned above. However, in the 2 kHz region it's the free field component that should dominate.
I tried to verify whether fixing the dominance of the ambient component in the 1200—3000 Hz band actually helps to fix the issue with "off-stage" positions, but I couldn't! Trying to correct this band both with Mid/Side equalization, and with the "phantom center" plugin couldn't affect the balance of fields, neither objectively (I re-measured with the same binaural approach), nor subjectively. I have concluded that either there must be some "destructive interference" happening to correlated signals, similar to room modes, or it's a natural consequence of head and torso reflections.
This is why subjective evaluations are needed. For comparison, this is how the balances between correlated and unilateral, and anti-correlated vs. correlated end up looking like in my headphone spatializer, overlaid with the previous graphs measured binaurally in the room, this is the direct component over unilateral signals:
This is the ambient component over direct:
Obviously, they do not look the same as their room-measured peers. The only similar feature is the peak in the diffuse component around 11 kHz (and I had to exaggerate it to achieve the desired effect).
You might have noticed two interesting differences: first, the level of the fully correlated sound for the spatializer is not much higher than levels of individual left and right channels. Otherwise, the center sounds too loud and close. Perhaps, this has something to do with a difference how binaural summing works in the case of dichotic (headphone) playback versus real speakers.
The second difference is in the level of bass for the ambient component. As I've found, enhancing the level of bass somehow makes the sound more "enveloping." This might be similar to the difference between using a mono subwoofer vs. stereo subwoofers in a room setup, as documented by Dr. Griesinger in his AES paper "Reproducing Low Frequency Spaciousness and Envelopment in Listening Rooms".
The other two "large-scale" parameters resulting from the spatial signal analysis that I needed to tune were the magnitude profile for the contra-lateral ear (the crossfeed filter), and the level of reverb. Let's start with the crossfeed filter which is linked to shoulder reflection simulation.
Shoulder Reflection Tuning And Crossfeed
The shoulder reflection I mentioned previously quite seriously affects the magnitude profile for all signals. Thus, if we intend to model the major peaks of valleys of the magnitude profile for the crossfeed filter, we need to take care of tuning the model of the shoulder reflection first. I start it objectively, by looking at the peaks in the ETC of the binaural recording. We are interested in the peaks that are located at approximately 500–700 microsecond delay—this is the approximate distance from the shoulder to the ear. Why not to use the exact distance measured on your body? Since we are not modeling this reflection faithfully, it will not sound natural anyway. So we can start from any close enough value and then adjust by ear.
There are other reflections, too: the closest to the main pulse are reflections from the ear pinna, and further down in time are wall reflections—we don't model these. The reason is that wall reflections are confusing, and in the room setup we usually try to get rid of them. And pinna reflections are so close to the main impulse, so they mostly affect the magnitude profile, which we adjust anyway.
So, above is the ETC graph of direct (ipsilateral) paths for the left ear. Contralateral paths are important, too (also for the left ear):
Torso reflections have rather complex pattern which heavily depends on the relative position of the source to the body (see the paper "Some Effects of the Torso on Head-Related Transfer Functions" by O. Kirkeby et al as an example). Since we don't know the actual positions of virtual sources in stereo encoding, we can only provide some ballpark estimation.
So, I started with an estimation from these ETC graphs. However, in order to achieve more naturally sounding setup, I've turned to listening. A reflection like this usually produces a combing effect. We hear this combing all the time, however we don't notice it because the hearing system tunes it out. Try listening to a loud noise, like a jet engine sound, or sea waves—they sound "normal." However, if you change your normal torso reflection by holding a palm of a hand near your shoulder, you will start hearing the combing effect. Similarly, when the model of the torso reflection is not natural, combing effect can be heard when listening to correlated or anti-correlated pink noise. The task it to tweak the timing and relative level of the reflection to make it as unnoticeable as possible (without reducing the reflection level too much, of course). This is what I ended up with, overlaid with the previous graphs:
Again, we can see that they end up being different from the measured results. One interesting point is that they have to be asymmetrical for left and the right ear, as this leads to more naturally sounding result.
Reverberation Level
Tuning the reverberation has ended up being an interesting process. If you recall previous posts, I use actual reverberation of my room, which sounds surprisingly good in the spatializer. However, in order to stay within the reverb profile recommended for music studios, I reduce its level to make it decay faster than in real room. Adding too much reverb can be deceiving because it makes the sound "bigger" and might improve externalization, however it also makes virtual sources too wide and diffuse. This of course depends on the kind of music you are listening to, and personal taste.
There are two tricks I've learning while experimenting. The first one I actually borrowed from Apple's spatializer. While analyzing their sound, I've found that they do not apply reverb below 120 Hz, like, at all. Perhaps, this is done to avoid effects of room modes. I tried that, and it somewhat cleared up the image. However, having no bass reverb makes the sound in headphones more "flat." I decided to add the bass back, but with a sufficient delay, in order to minimize its effect. I also limited it application to "ambient" components only. As a result, the simulated sound field has become wider and more natural. Below are reverb levels for my room, my processing chain, and for comparison purpose, captured from Apple's stereo spatializer, playing through AirPods Pro.
The tolerance corridor is calculated for the size of the room that I have.
We can see that for my spatializer, the reverb level is within the studio standard. And below is the Apple's reverb:
A great advantage of having your own processing chain is that you can experiment a lot, something that is not really possible in a physical room and with off-the-shelf implementations.
Tuning the Headphones
As I've mentioned, I found Zero:Red by Truthear to be surprisingly good for listening to the spatializer. I'm not sure whether this is due to their low distortion, or due to their factory tuning. Nevertheless, the tuning has still to be corrected.
Actually, before doing any tuning, I had to work on the comfort. These Zero:Reds have quite a thick nozzle—larger than 6 mm in diameter, and with any stock ear tips they were hurting my ear canals. I found tips with thinner ends—SpinFit CP155. With them, I almost forget that I have anything insert into my ears.
Then, the first thing to tune was to reduce the bass. Ideally, the sensory system should not be able to detect that the sound is originating from the source close to your head. For that, there must be no vibration perceived. For these Zero:Reds I had to reduce overall bass region by 15 dB down, plus address individual resonances. A good way to detect them is to run a really long logarithmic sweep through the bass region. You would think that reducing the bass that much makes the sound too "lightweight," however, the bass from reverb and late reverb does the trick. In fact, one interesting feeling that I get is the sense of floor "rumbling" through my feet! Seriously, first couple of times I was checking if I accidentally left the subwoofer on, or is it vibration from the washing machine—but in fact this just is a sensory illusion. My hypothesis is that there are perception paths that help to hear the bass by feeling it with body, and these paths are at least partially bidirectional, so hearing the bass in headphones "the right way" somehow can invoke a physical feeling of it.
All subsequent tuning was more subtle and subjective, based on listening to many tracks and correcting what wasn't sounding "right." That's of course not the best way to do tuning, but it worked for me on these particular IEMs. After doing the tweaking, I have compared the magnitude response of my spatializer over Zero:Reds with Apple's spatializer over AirPods. In order to be able to compare "apples to apples," I have measured both headphones using the QuantAsylum QA490 rig. Below is how the setup looked like (note that on the photo, I have ER4SRs inserted into QA490, not Zero:Reds):
And here are the measurements. Note that since QA490 is not an IEC-compliant ear simulator, measured responses can only be compared to each other. The upper two graphs are for the left earphone, the lower two are for the right headphone, offset by -15 dB. Measurements actually look rather similar. AirPods can be distinguished by having more bass, and I think that's one of the reasons why to my ears they sound less "immersive" to me:
Another likely reason is that I tend to use linear phase equalizers, at the cost of latency, while Apple spatializer likely uses minimum phase filters which modify timing relationships severely.
Conclusion
Creating a compelling, and especially "believable" stereo spatialization is anything but easy. Thankfully, these days even at home it is possible to make measurements that may serve as a starting point for further adjustment of the processing chain. A challenging part is finding headphones that would allow disappearing in one's ears, or on one's head, as concealing them from the hearing system is one of the prerequesites for tricking the brain that the sound is coming from around you.