A while ago I was checking how Google Play Music and the playback chain following it are handling intersample peaks. Since then, GPM was retired and replaced with YouTube Music (YTM), browsers got uncountable number of updates, and so on. Did the situation with digital headroom improve? I was stimulated to check this by the fact that I tried using YTM in Chrome browser on my Linux laptop, and was disappointed with the quality of the output. Before that, I was using YTM on other OSes, and it was sounding fine. Is there anything wrong with Linux? I decided to find out.
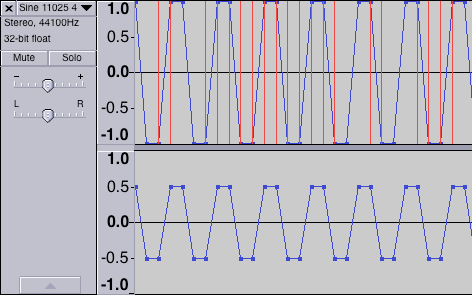
I have updated my set of test files. I took the same test signal I used back in 2017: a stereo file where both channels carry a sine at the quarter of the sampling rate (11025 or 12000 Hz), with a phase shift at 45 degrees. The left channel has this signal normalized to 0 dBFS, and this creates intersample overs peaking at about +3 dBFS, and the right channel has this signal at the half of the full scale (6 dB down), which provides enough headroom and should survive any transformations:
I have produced a set of test files to include all the combinations of the following attributes:
- sample rate: 44.1 and 48 kHz;
- bit width: 16 and 24;
- dither: none and triangular.
There are two things that I can validate using these signals: non-linearities introduced by clipping or compression of intersample peaks, and whether the inter channel balance stays the same. For measuring non-linearities I used the THD+N measurement. Although, due to the fact that the signal is at the quarter of the sampling rate, even the second harmonic is out of frequency range, the "harmonic distortion" part of this measurement doesn't make much sense, however the "noise" part still does. There is a strong correlation between the look of the frequency response graph and the value of the THD+N.
I have uploaded my test signals to YouTube Music and then measured the THD+N in the following clients:
- the official web client running in recent stable versions of Chrome and FireFox on Debian Linux, macOS, and Windows,
- and the official mobile apps running on an Android phone (Pixel 5) and iPad Air.
All the outputs were measured using a digital capture chain. For macOS and Windows I used a hardware loopback on RME FireFace card. For Linux I used Douk Audio USB to S/P-DIF digital interface (Mini XMOS XU208) which was connected by optics to the FireFace card. For mobile devices I used a dual USB sound card iConnectAudio4 by iConnectivity. The sound cards were configured either at 44.1 or at 48 kHz.
Observations and Results
The first thing I've noted was that YouTube Music stores audio tracks at 44.1 kHz sample rate (this is confirmed by looking at the "Encoding Specifications" in the YT tech support pages), and 48 kHz files got mercilessly resampled, clipping the channel with overs quite severely. This can be easily seen by comparing the difference between the L&R channels of the signal played back—it's only 4.34 dB instead of 6 dB. Below is the spectrum of the 48 kHz test signal after it has went through YTM's server guts:
Also, it can be seen from the graph, YTM does some "loudness normalization" by scaling the amplitude of the track down, likely after resampling it to 44.1 kHz. This causes the peaks on both channels to be down by about 11 dB. Actually, that's good because it provides needed headroom for any sample rate conversions happening after the tracks leave the YTM client.
As for the lossy compression, it actually doesn't add much artifacts, as we can see from this example:
Yes, there is a "bulb" around the original signal likely added due to the fact that the codec works in the frequency domain and has reduced resolution. However, the THD+N of this signal is just 3 dB down (-103.4 dB) from the 16-bit dithered original (-106.8 dB), and it's still on par with capabilities of good analog electronics. So, lossy codec is not on the list of my concerns for the content on YTM.
Desktop Clients
On desktop, the difference in the measurements only depends on the browser. However, the trouble with Linux is that both Chrome and FireFox always switch the output to 48 kHz as they start playing even if the PulseAudio daemon is configured to use 44100 Hz for both the "default" and "alternative" sample rates. As we will see, this does a bad job for Chrome and likely was the reason why I felt initially that something is going wrong with YTM on Linux.
Yet another interesting observation on the desktop is that in case the browser does a bad job of resampling, bringing the digital volume control down on the YTM client does not provide any extra headroom for the browser's processing. That was a bummer! Apparently, the order of the processing blocks has changed, compared to Play Music, putting the digital attenuation after resampling, maybe because YTM uses some modern web audio API which gives the browser more control over media playback.
Here is a summary of THD+N measurements for Chrome and FireFox for cases when the system output is either at the "native" sampling rate—44.1 kHz or at 48 kHz. On the left there are baseline numbers for the original dithered signal, measures for the left and the right channel are delimited with a common slash:
| Signal | Chrome to 44 | Chrome to 48 | FireFox to 44 | FireFox to 48 |
|---|---|---|---|---|
| 24/44, -146.7 / -139.2 | -102.7 /-103.7 | -29.6 / -82.6 | -103.4 / -103.7 | -103.3 / -103.5 |
| 16/44, -106.8 / -95.5 | -102.9 / -97.8 | -29.6 / -82.5 | -102.1 / -97.8 | -102.3 / -97.6 |
| 24/48, -147.5 / -139.7 | -17.7 / -98.4 | -17.7 / -80.6 | -17.7 / -98.4 | -17.7 / -98.4 |
| 16/48, -106.7 / -95.6 | -17.7 / -89.4 | -17.7 / -79.7 | -17.7 / -89.5 | -17.7 / -89.3 |
As we can see here, Chrome doesn't do a good job when it has to resample the output to 48 kHz, thus on Linux the only option is to use FireFox instead of it. And obviously, even FireFox can't undo the damage done to the original 48 kHz signal with intersample overs.
My guess would be that the audio path on FireFox uses floating point processing which creates necessary headroom, while Chrome still uses integer arithmetic.
Mobile Clients
Results from iOS are on par with FireFox confirming that this is likely the best result we can achieve with YTM. Android adds more noise:
| Signal | Android to 44 | Android to 48 | iOS to 44 | iOS to 48 |
|---|---|---|---|---|
| 24/44, -146.7 / -139.2 | -92.9 / -92.2 | -92.9 / -92.2 | -102.8 / -102.2 | -102.8 / -102.2 |
| 16/44, -106.8 / -95.5 | -92.6 / -88.3 | -92.6 / -88 | -101.8 / -97.7 | -102 / -97.7 |
| 24/48, -147.5 / -139.7 | -17.7 / -92 | -17.7 / -92 | -17.7 / -98.5 | -17.7 / -98.5 |
| 16/48, -106.7 / -95.6 | -17.7 / -87.9 | -17.7 / -87.8 | -17.7 / -89.4 | -17.7 / -89.4 |
I had a chance to peek "under the hood" of Pixel 5 by looking at the debug dump of the audio service. What I could see there is that there are extra sample rate conversions happening on the way from the YTM app to the USB sound card. The app creates audio tracks with 44100 Hz sample rate. However, the USB audio on modern Android phones is managed by the same SoC audio DSP used for built-in audio devices, to bring down latency when using USB headsets. The DSP works at 48 kHz. Thus, even when the USB sound card is at 44.1, the audio tracks from YTM first got upsampled to 48 kHz to get to the DSP, and then DSP downsamples them back to 44.1 kHz for the sound card. I guess, on Apple devices either this pipeline is more streamlined, or everyone (including the DSP) use calculations providing enough headroom.
Conclusions
I think, it is all pretty clear, but here is the summary how to squeeze out the best quality from YouTube Music:
- on desktop, when using Chrome (or Edge on Windows), set the sampling rate of the output to the native sample rate of YTM: 44.1 kHz, if that's not possible, use FireFox;
- on Linux, always use FireFox instead of Chrome for running YTM client, because even lowering the digital volume on the YTM client does not prevent from clipping;
- due to the fact that YTM applies volume normalization, there is no need to worry about having digital headroom on the DAC side;
- any 48 kHz or higher content needs to be carefully resampled to 44.1 kHz before uploading to YTM to prevent damage from their sample rate conversion process.